Курсовая работа: Динамический синтез систем автоматического управления

Используем передаточную функцию разомкнутой системы (1.10)

Для получения частотной передаточной функции заменим S на jw и преобразуем

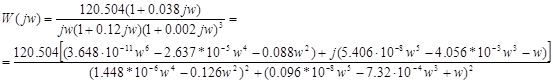
Вещественная и мнимая части соответственно:

(1.11) ; (1.12)

Тогда

.

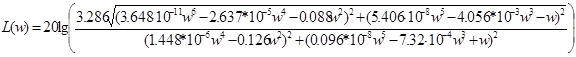
ЛАЧХ и ЛФЧХ разомкнутой системы представлены ниже.

ЛАЧХ скорректированной системы сместилась вправо, следовательно, необходимые требования по точности выполняются, запасы устойчивости увеличились по сравнению с системой с пропорциональным регулятором.

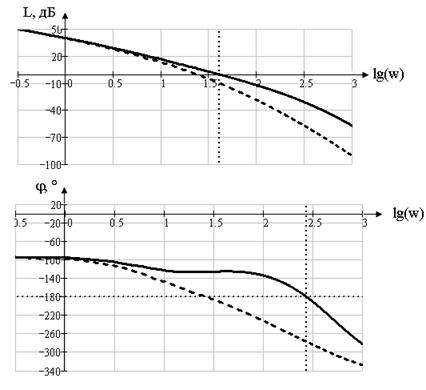
–– ЛАЧХ и ЛФЧХ скорректированной системы

- - ЛАЧХ и ЛФЧХ системы с пропорциональным регулятором

Рисунок 1.15 ЛАЧХ и ЛФЧХ систем

Построим график АФЧХ по имеющимся формулам (1.11) и (1.12) и сравним его с графиком системы с пропорциональным регулятором. Он представляет собой годограф Найквиста, поэтому сделаем ниже дополнительно выводы об устойчивости системы.

Составим таблицу, изменяя w от 0 до ∞:

Таблица 1.3

W ,	P(w)	Q(w)
0	-10,604	-∞
852,2	0	5,806*10-3
274,2	-0,094	0
	0	0

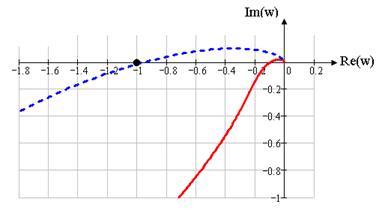
–– годограф скорректированной системы

- - годограф системы с пропорциональным регулятором

Рисунок 1.16 – Годограф Найквиста

Характеристическое уравнение имеет вид:

Все корни характеристического уравнения, кроме одного нулевого, левые, следовательно, разомкнутая система на границе устойчивости. Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывал особу точку (-1; j0). Данное условие выполняется, значит, замкнутая система устойчива.

Построим годограф Михайлова для системы.

Передаточная функция замкнутой системы:

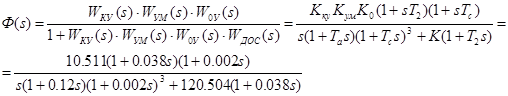(1.13)

Функция Михайлова имеет вид:

(1.14)