Курсовая работа: Динамический синтез систем автоматического управления
Таблица 1.1
| w | P | Q |
| 0 | -11.25 | -¥ |
| 234.5 | 0 | 4,584*10- 3 |
| 26.2 | -0.95 | 0 |
| ¥ | 0 | 0 |
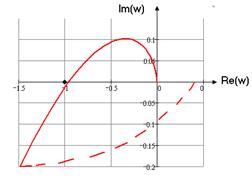
Рисунок 1.8 Годограф Найквиста
Из рисунка видно, что замкнутая система устойчива.
Проверим устойчивость замкнутой системы по логарифмическим частотным характеристикам.
Построим логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ).
[1, § 4.4]
Определим модуль частотной передаточной функции для разомкнутой системы:
![]() ;
;
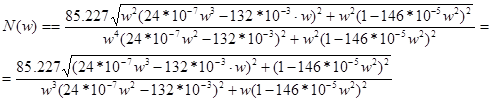 (1.7)
(1.7)
Определим L ( w ) и ![]()
![]() ;
;
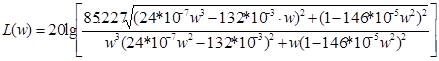 ;
;
![]()
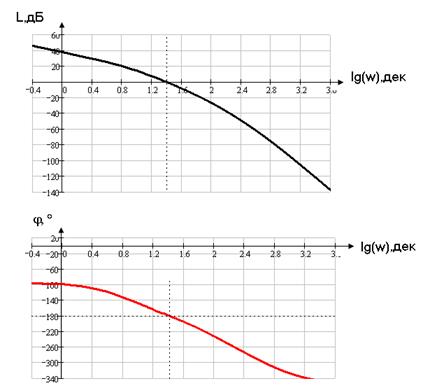
Рисунок 1.9 ЛАЧХ и ЛФЧХ системы с регулятором
Видно, что точка пересечения ЛФЧХ с линией -180о лежит немного правее точки пересечения ЛАЧХ с осью абсцисс. Следовательно, замкнутая система устойчива.
Проверим систему на устойчивость по критерию Михайлова. [1, § 6.3]
Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова начинался на вещественной положительной полуоси и при увеличении частоты последовательно проходил число четвертей, соответствующее порядку системы (нигде не обращаясь в 0).
Функция Михайлова для нашей системы:
![]()
Выделим вещественную и мнимую части:
![]() ;
;
![]()
Построим годограф Михайлова по следующим значениям:
Таблица 1.2
| w , | X ( w ) | Y ( w ) |
| 0 | 85,227 | 0 |
| 25,6 | 0 | 1,105 |
| 26,2 | -4,252 | 0 |
| 233,1 | 0 | -1,8259∙104 |
| ∞ | -∞ |
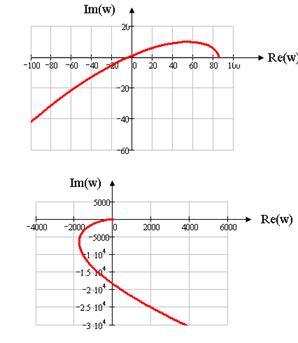
Рисунок 1.10 Годограф Михайлова для малых и больших частот соответственно
Следовательно, система устойчива.