Курсовая работа: Исследование линейных и нелинейных систем управления
Inf 36.0532
Таблица 3 – Запас устойчивости САР
| Регуляторы | ∆L | ∆φ |
| П | ¥ | 41.6 |
| ПИ | ¥ | 36.7 |
| ПИД | ¥ | 36.1 |
Проанализировав полученные данные, можно сделать вывод, что необходимым запасом устойчивости и по амплитуде, и по фазе обладают все САР.
3 Оценка управляемости и наблюдаемости линейной САР
3.1 Анализ САР с П-регулятором
3.1.1 Разработка математической модели типа «вход-состояние-выход»
Основная передаточная функция САР с П-регулятором была получена в п. 1.3. Она имеет вид:
,
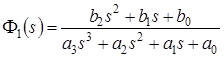где 
,
Порядок характеристического полинома 
. Для данной САР выбираем вторую управляемую форму или управляемое каноническое представление (УКП). Математическая модель САР описывается следующей системой векторно-матричных уравнений:
 |
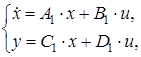где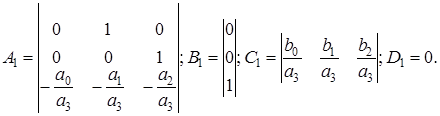
Script 12:
>> b2=2.397;b1=18.64;b0=5.859;
>> a3=336;a2=148.4;a1=39.64;a0=6.859;
>> A1=[0 1 0;0 0 1;-a0/a3 -a1/a3 -a2/a3];
>> B1=[0;0;1];
>> C1=[b0/a3 b1/a3 b2/a3];
>> D1=0;
>> sys1=ss(A1,B1,C1,D1)
a =
x1 x2 x3
x1 0 1 0
x2 0 0 1
x3 -0.02041 -0.118 -0.4417
b =
u1
x1 0
x2 0
x3 1
c =