Реферат: Анализ обобщенных функций
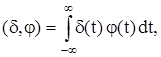 (2)
(2)
где j (t) – основная функция. Скалярное произведение (2.) есть линейный непрерывный функционал на пространстве основных функций (jÎK). Функция d(t) называется дельта – функцией (обобщенная функция Дирака).
Определим произведение обобщенной функции fна число lсоотношением
(lf, j) = l (f, j) ( jÎK).
Сумма двух обобщенных функций f1 , f2 определим следующим образом
(f1 + f2 , j) = (f1 , j) + (f2 , j) ( jÎK).
После этого множество обобщенных функций K' становится линейным пространством.
Определение. Две обобщенные функции f(t), g(t) ÎK' равны: f(t) = g(t), если для любой основной функции j (t)
(f, j) = (g, j) или (f– g, j) = 0.
Обобщенная функция f(t) равна нулю: f= 0, если для любой основной функции j (t)
(f, j) = 0.
Примеры обобщенных функций.
1. Пусть jÎK. Определим обобщенную функцию fс помощью функционала
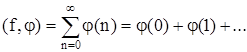
Приведенная сумма конечна, так как основная функция j(t) равна нулю вне некоторого конечного интервала.
2. Введенную ранее дельта-функцию d(t) определим следующим образом
(d(t), j(t)) = j(0).
Исходя из интегрального представления (2), имеем
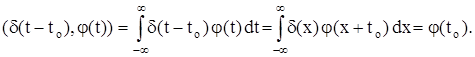
Если а(t) – непрерывная функция, то
(а(t) d(t), j(t)) = (d(t), а(t) j(t)) = a(o) j(o) ( jÎKo ).
Отметим, что функционал f, определенный на Kсоотношением
![]()
не является обобщенной функцией, так как, являясь непрерывным функционалом, он не линеен.
3. Обобщенная функция Хевисайда
![]()
для которой можно записать
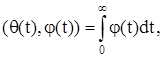
является регулярной обобщенной функцией.
2.Действия над обобщенными функциями