Реферат: Анализ обобщенных функций

Поэтому

6. Пространство обобщенных функций

Совокупность обобщенных функций, порождаемых основным пространством K, образует пространство K'. Рассмотрим подпространство обобщенных функций пространства K, состоящее их обобщенных функций, равных нулю вне некоторого конечного интервала принадлежащего [0, ¥]. Введем в этом пространстве операцию умножения двух функций в виде свертки этих функций. Если f(t), g(t) Î то и Кроме того свертка обладает всеми свойствами обычной операции умножения. Роль единицы в играет функция d(t), так как для

Пусть существует такая что

тогда f^-1 (t) называется обратной обобщенной функцией f(t).

Пространство с введенной операцией умножения образует алгебру (коммутативную) со сверткой.

Рассмотрим алгебру со сверткой . Обобщенная функция так как она равна нулю всюду, кроме точки ноль. Обобщенная функция сосредоточена вначале координат, поэтому Далее,

поэтому

Теорема. Пусть для существуют обратные функции f^{- 1} (t) и g^-1 (t). Тогда свертка имеет обратную функцию вида

Действительно,

Рассмотрим следующее определенное в уравнение в свертках

Свертка существует для любой обобщенной функции так как

Следовательно, y(t) является фундаментальным решением уравнения (4). В частности, фундаментальное решение уравнения (6) с оператором 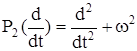принадлежит алгебре со сверткой Следовательно,

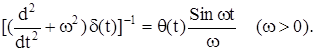
Рассмотрим операционный метод решения уравнения в свертках. Пусть имеется уравнение

где a(t) и b(t) Î Среди эффективных методов решения этого уравнения приведем метод преобразования Лапласа. Применив преобразование Лапласа к левой и правой части этого уравнения, имеем

Отсюда следует