Реферат: Анализ обобщенных функций

Можно вычислить производные

(t₊ )' = q(t), (t_- )' = -q(-t),

а также

n

2.1 Свертка обобщенных функций

Пусть f(t) и g(t) - интегрируемые на любом конечном интервале функции. Свертка функций f(t) и g(t) определяется соотношением

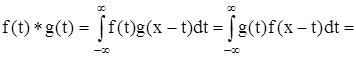
если только интеграл существует и интегрируем по любому конечному интервалу переменной х. Равенство двух интегралов легко проверить, сделав замену z= x-t.

Если f(t), g(t) – регулярные обобщенные функции и j(х) ÎK, то можно записать

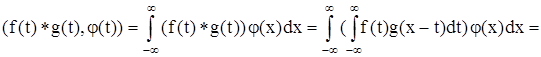
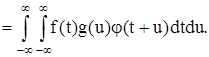
Произведение f(t) g(u) можно рассматривать как прямое произведение f(t) х g(u), так что

Это соотношение определяет свертку обощенных функций f(t), g(t) ÎK', включая и сингулярные обобщенные функции.

Свертка обобщенных функций обладает следующими свойствами:

1)

2)

3)

4) если 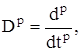то

(3)

Приведем доказательство последнего соотношения. Действительно, для j(х) Î K

или

что и доказывает соотношение (3).

Примеры: