Реферат: Анализ обобщенных функций

(g'(t), j(t)) = (f(t), j(t)).

Если f(t) – сингулярная обобщенная функция, то возможны случаи, когда ее первообразная – регулярная обобщенная функция. Например, первообразная d(t) является y(t) = q(t); первообразная q(t) является функция y(t) = t₊ , а решение уравнения

y''(t) = d(t)

можно записать в виде

t(t) = t₊ + C₁ t + C₂ (C₁ , C₂ = const).

Рассмотрим линейное уравнение n-го порядка с постоянными коэффициентами

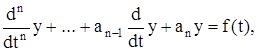(4)

где f(t) – обобщенная функция. Обозначим

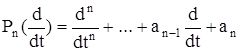
дифференциальный полином n-го порядка.

Определение. Обобщенным решением дифференциального уравнения (4) называется обобщенная функция y(t), для которой выполняется соотношение

Если f(t) – непрерывная функция, тогда единственным решением уравнения (4.) является классическое решение.

Определение. Фундаментальным решением уравнения (4) называется любая обобщенная функция e(t) такая, что

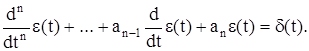
Функция Грина – фундаментальное решение, удовлетворяющее данному граничному, начальному или асимптотическому условию.

Теорема. Решение уравнения (4) существует и имеет вид

(5)

если только свертка определена.

Доказательство. Действительно,

По свойству свертки имеем

В качестве примера рассмотрим уравнение

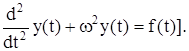(6)

Нетрудно видеть, что фундаментальным решением этого уравнения является

так как