Реферат: Билеты по предмету Математические методы в экономике за осенний семестр 2000 года

Достаточные условия минимума функции двух переменных.

В чем состоит задача принятия решения?

В игре двух лиц с нулевой суммой матрица выигрышей Н равна:
Н = Чему равна нижняя цена игры?

Найти частную производную второго порядка по х функции
f(x,y) =12xy² + х + 4х³у - 3.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ

Билет № 29

1. Привести свойства операций сложения матриц и умножения матрицы на число.

2. Записать в общем виде задачу линейного программирования на максимум в стандартной форме, если размерность задачи: две переменных, одно ограничение.

3. Область определения функции нескольких переменных.

4. Дать понятие безусловного экстремума функции нескольких переменных.

5. Условия Куна-Таккера.

6. Для матриц Ax и B записать условие Ax  B в виде системы неравенств, если , , .

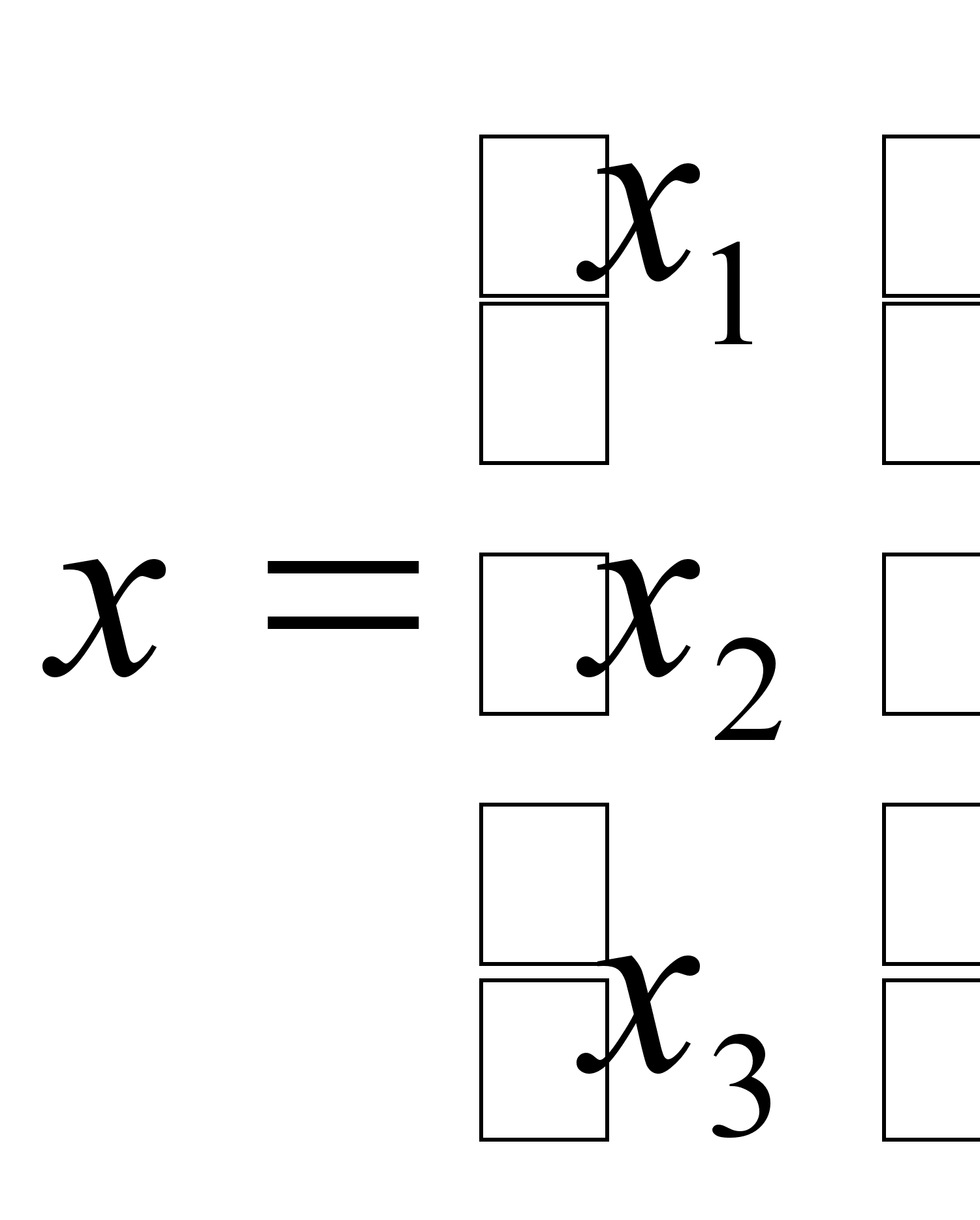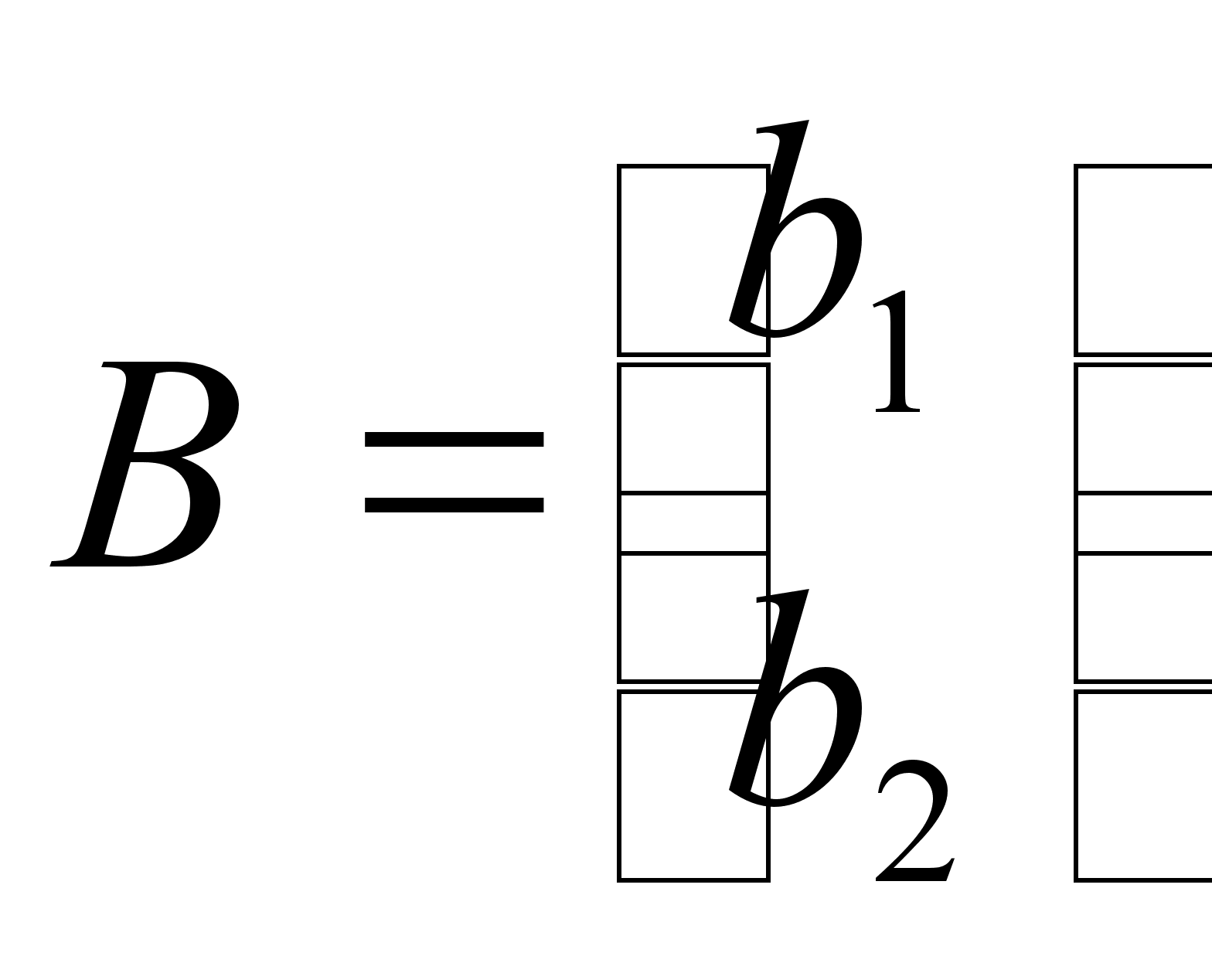7. Для следующей задачи выпуклого программирования
   
   построить функцию Лагранжа.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ

Билет № 30

1. Дать определение степени матрицы.

2. Привести функцию дохода в задаче составления плана производства.

3. Привести основные понятия теории игр.

4. Частные производные высших порядков функции нескольких переменных.

5. Дать понятие оценки альтернативы х по критерию.

6. Известны вектор цен потребительских товаров p = (30, 48, 5) и вектор количества потребляемых товаров q = (2, 2, 25). Найти скалярное произведение и указать смысл скалярного произведения векторов p и q.

7. Найти частную производную первого порядка по у функции
   f(x,y) =12xy² + х + 4х³у - 3.