Реферат: Билеты по предмету Математические методы в экономике за осенний семестр 2000 года
Необходимые и достаточные условия экстремума функции двух переменных.
Градиент функции двух переменных. Определение, свойства.
Однородность функции двух переменных степени r.
Задача нелинейного программирования. Постановка.
Понятие выпуклых функций и выпуклых множеств. Задача выпуклого программирования. Постановка. Свойства.
Схема градиентных методов решения задачи выпуклого программирования. Метод наискорейшего спуска.
Функция Лагранжа задачи выпуклого программирования. Множители Лагранжа.
Условия Куна-Таккера.
Задача динамического программирования.
Метод динамического программирования. Принцип оптимальности Боллмана. Область применения динамического программирования.
Задача стохасического программирования в жесткой постановке и по средним.
Задачи экономики.
Постановка задачи принятия решения. Участники задачи принятия решения.
Методы обработки экспертной информации.
Для векторов x = (1, 0, 2, 4, 7), y = (0, 2, 4, 1, 1) указать размерность, построить векторы 2x, 5y, 3x + 2y, вычислить (x, y), (3x, 2y), (2x + y, x + 2y).
Для матриц А =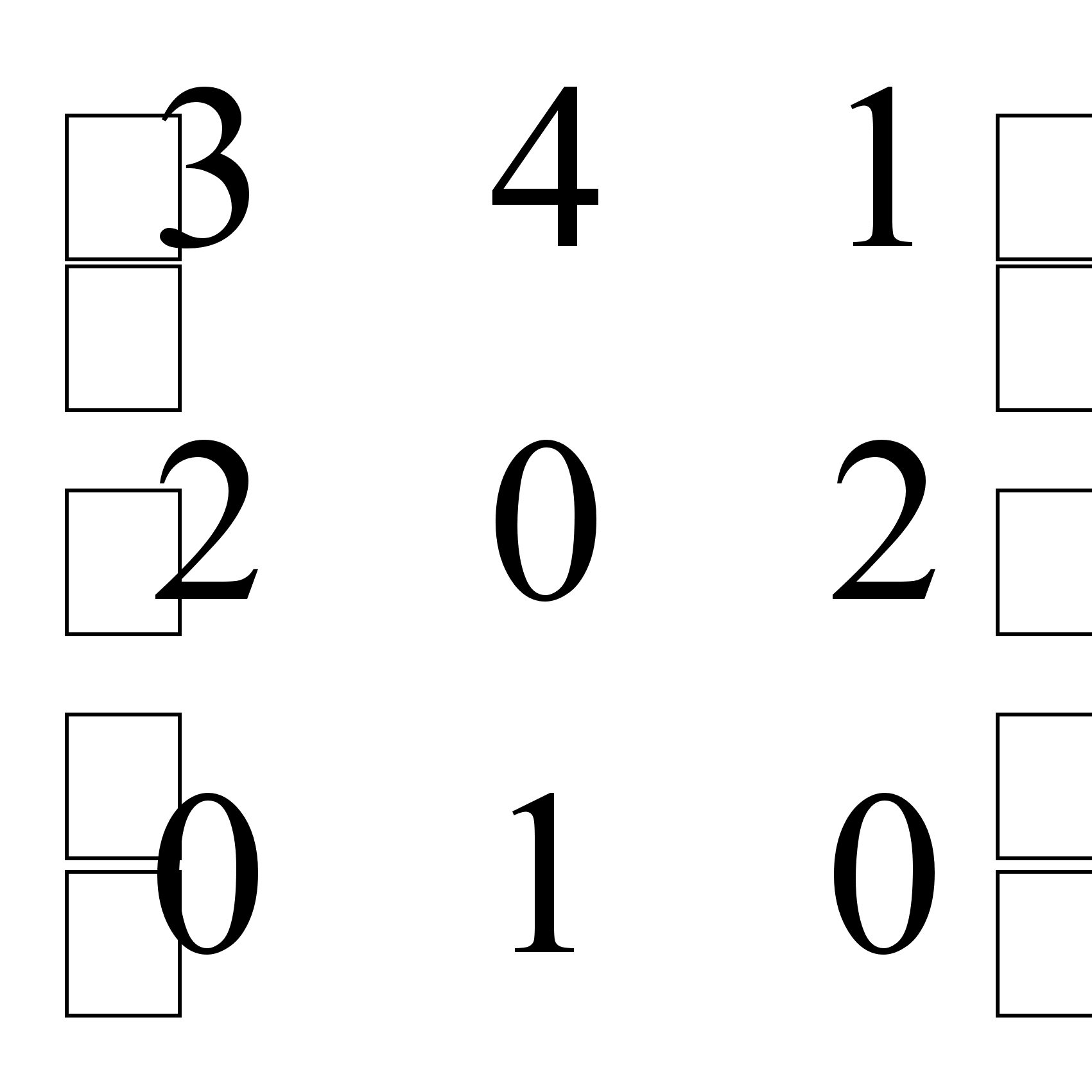 
, В = 
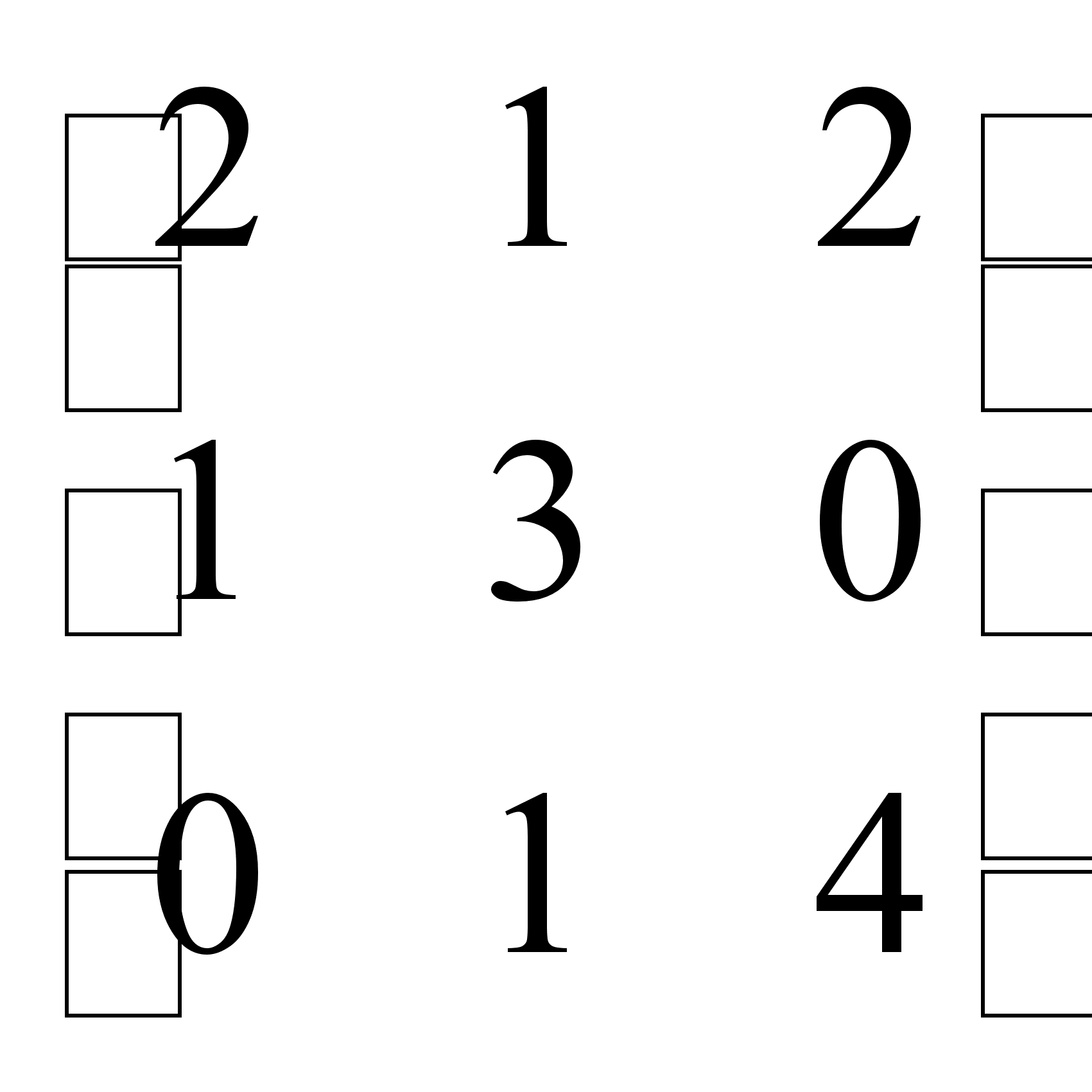найти А + В, 3А + 4В, В', А·В, В·А, |A|, A-1.
Систему уравнений записать в матричной форме: 
. Решить.
Решить задачу линейного программирования: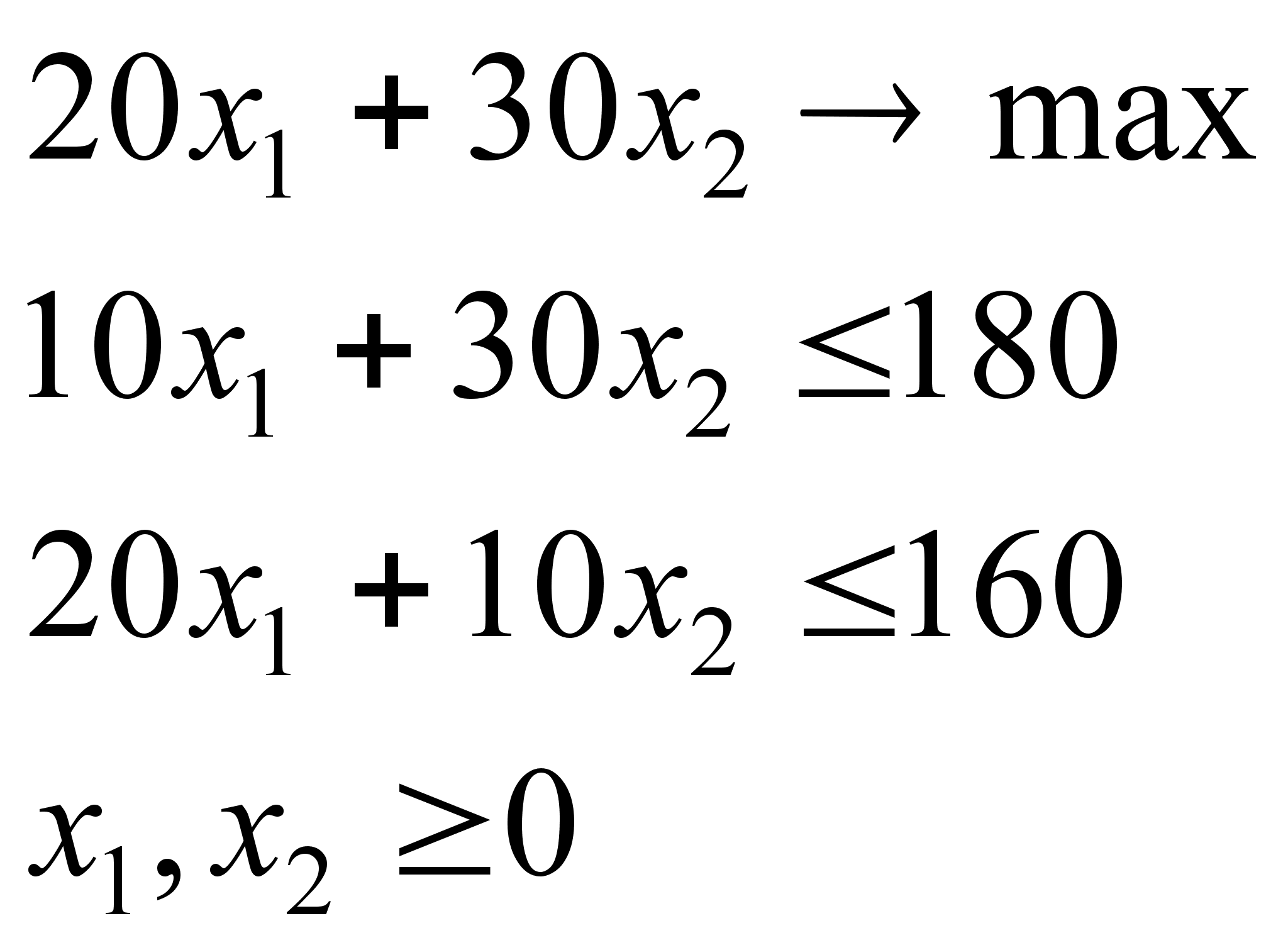 
. Указать оптимальное решение (x1, x2), максимальное решение целевой функции 20x1 + 30x2. Построить двойственную и найти ее решение. Дать геометрическую иллюстрацию, интерпретацию условий двойственности.
В игре двух лиц с нулевой суммой с матрицей выигрышей Н =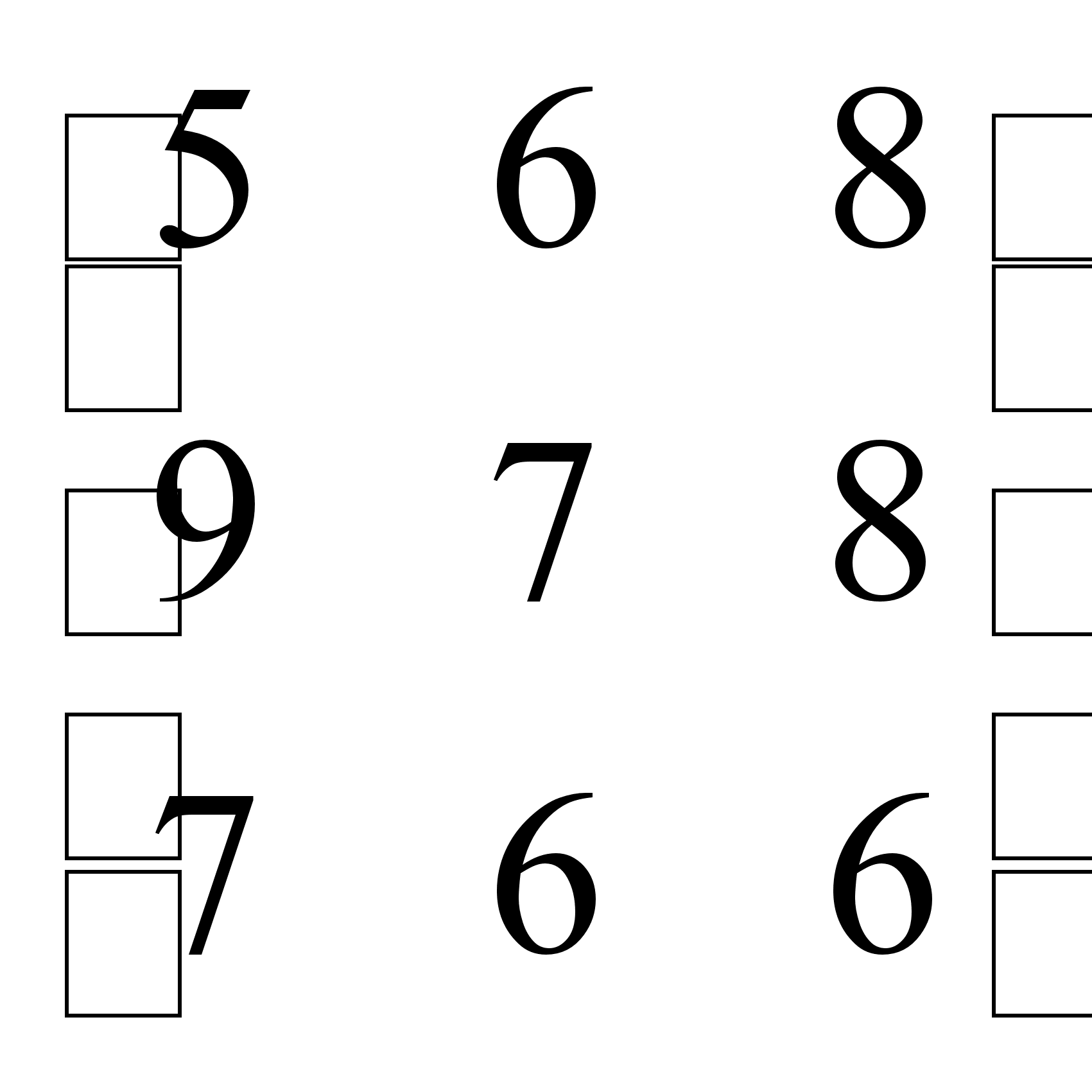 
указать: ― число стратегий первог