Реферат: Интеграл Лебега

£ .

Действительно, функция F( x)— f( x) не отрицательна, так что

- = ³ 0.

Теорема 6. Если функция f( x) измерима и ограничена на измеримом множестве E, то

£

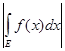4. Предельный переход под знаком интеграла

Здесь мы рассмотрим следующий вопрос: пусть на измеримом множестве E задана последовательность измеримых ограниченных функций

f₁ (x), f₂ (x), f₃ (x), ¼ , f_n (x), ¼

которая в каком-нибудь смысле (везде, почти везде, по мере) схо­дится к измеримой ограниченной функции F( x). Спрашивается, будет ли справедливо соотношение

= (1)

Если (1) верно, то говорят, что допустим предельный переход под знаком интеграла.

Легко видеть, что, вообще говоря, это не так. Например, если функции f_n ( x) определены в сегменте [0, 1] следующим образом:

n при x Î ,

f_n ( x) =

0 при x ,

то при всяком x Î [0, 1] будет

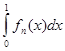f_n ( x) = 0, но = 1,

и этот интеграл не стремится к нулю.

Поэтому естественно поставить вопрос о тех дополнительных ограничениях, которые нужно наложить на функцию f_n ( x), чтобы равенство (1) все же имело место.

Мы ограничимся доказательством следующей теоремы.

Теорема (А. Лебег). Пусть на измеримом множестве Е за­дана последовательность f₁ ( x), f₂ ( x), f₃ ( x), ¼ измеримых огра­ниченных функций, сходящаяся по мере к измеримой ограниченной функции F(х)

f_n (x) Þ F(x).

Если существует постоянная К, такая, что при всех п и лри всех х

< K,

то

= (1)

Доказательство. Прежде всего заметим, что почти для всех х Î Е будет

£ K. (2)

В самом деле, из последовательности { f_n ( x)} можно (на основании теоремы Рисса) извлечь частичную последовательность {( x)}, которая сходится к F( x) почти везде. Во всех точках, где