Реферат: Интеграл Лебега

1 при x ³ 0,

f( x) =

-1 при x < 0,

то

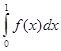= + = -1 + 1 = 0,

хотя функция f( x) и не эквивалентна нулю.

Однако справедливо

Следствие 2. Если интеграл от неотрицательной из­меримой ограниченной функции f( x) равен нулю

( f( x) ³ 0),

то эта функция эквивалентна нулю.

В самом деле, легко видеть, что

E( f >0) = .

Если бы f( x) не была эквивалентна нулю, то необходимо на­шлось бы такое n₀ , что

mE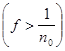 = s > 0.

Полагая

A = E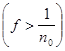, B = B - A,

мы имели бы, что

³ s, ³ 0,

и, складывая эти неравенства, мы получили бы

³ s,

что противоречит условию.

Теорема 3. Если на измеримом множестве Q заданы две измеримые ограниченные функции f( x) и F( x), то

= + .

Теорема 4. Если на измеримом множестве Е задана изме­римая ограниченная функция f( x) и с есть конечная постоянная, то

= c.

Следствие. Если f( x) и F(х) измеримы и ограничены на мно­жестве Е, то

= - .

Теорема 5. Пусть f( x) и F(х) измеримы и ограничены на измеримом множестве Е. Если

f(x) £ F(x),