Реферат: Интеграл Лебега

можно перейти к пределу в неравенстве < K, что и при­водит к (2).

Пусть теперь s есть положительное число. Положим,

A_n ( s) = E( ) ³ s), B_n ( s) = E( ) < s.

Тогда

£ = + .

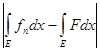В силу неравенства £ + , почтидля всех х из множества A_n ( s) будет

< 2 K,

так что по теореме о среднем

£ 2 K × mA_n ( s) (3)

(то обстоятельство, что неравенство < 2К может не выпол­няться на множестве меры 0, несущественно. Можно, например, функцию на этом множестве изменить, сделав ее равной нулю; тогда неравенство (3) будет выполняться во всех точках А. Но так как изменение функции на множестве меры 0 не влияет на величину интеграла, то (3) верно и без такого изменения).

С другой стороны, опять-таки в силу теоремы о среднем,

£ s mB_n ( s) £ s mE.

Сопоставляя это с (3), находим, что

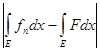£ 2K × mA_n ( s ) + s mE. (4)

Заметив это, возьмем произвольное e > 0 и найдем столь малое s> 0 , что

s × mE < .

Фиксировав это s , мы, на основании самого определения сходи­мости по мере, будем иметь, что при n ® ¥

mA_n ( s) ® 0

и, стало быть, для n > N окажется

2 K × mA_n ( s) < .

Для этих n неравенство (4) примет вид

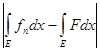< e,

что и доказывает теорему.

Легко понять, что теорема остается верной и в том случае, когда неравенство

< K

выполняется только почти везде на множестве Е. Доказательство остается прежним.

Далее, поскольку сходимость по мере общее обычной сходи­мости, то теорема и подавно сохраняет силу для того случая, когда

f_n (x) ® F(x)

почти везде (и тем более везде).