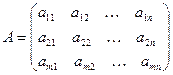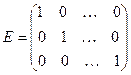Математика / Реферат: Матрицы и определители 3

Реферат: Матрицы и определители 3

Вычислите определитель матрицы и убедитесь, что он не равен нулю

D(А) = 6+1+0+4+0-0 = 11 ¹ 0

2 Найти алгебраические дополнения элементов матрицы А

А₁₁ = 6 А₁₂ = -1 А₁₃ = 2

А₂₁ = -3 А₂₂ = -5 А₂₃ = +1

А₃₁ = 5 А₃₂ = +1 А₃₃ = -2

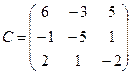
3 Составить транспонированную матрицу из алгебраических дополнений

Найти обратную матрицу

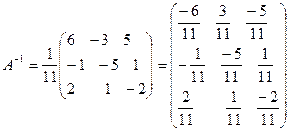
Убедиться, что обратная матрица найдена верно

А^-1. А = Е

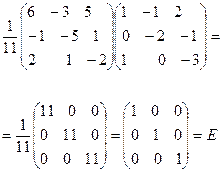
Решите самостоятельно.

Вычислить обратную матрицу .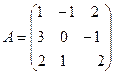

Задания для самостоятельной работы

Самостоятельно решите следующую задачу:

Даны две матрицы

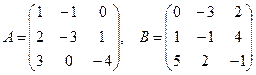
Построить матрицу С.
Найти определитель матрицы С.
Найти матрицу, обратную к матрице С.
Найти произведение матриц А и С.

№ вар	С	№ вар	С
1	2А-3В + А^Т	11	-2А+В+2А^Т
2	А+2В+В^Т	12	-3А+4В-3В^Т
3	-2А-В+2А^Т	13	-А+3В+4А^Т
4	3А-В+В^Т	14	2А+4В-В^Т
5	А-3В+2А^Т	15	3А-В+А^Т
6	3В-2А-ВТ^Т	16	2А+5В-2А^Т
7	2А+В-А^Т	17	3А-В-3В^Т
8	2В-2А+3В^Т	18	4А+2В-А^Т
9	4А+В-2А^Т	19	2А+3В+2А^Т
10	-2А+4В+В^Т	20	2А-3В-В^Т

ГЛОССАРИЙ

№	Новые понятия	Содержание
1	Прямоугольная матрица порядка mn, обозначаемая	Прямоугольная таблица из mn действительных чисел, где первое число m равно числу строк, а n – числу столбцов матрицы А; коротко матрица А обозначается А = (а_ik )_mn
2	Элементы матрицы	числа а_ik , из которых состоит матрица; индексы определяют положение элемента в таблице; первый индекс i – номер строки, второй k – номер столбца, на пересечении которых стоит элемент а_ik
3	Квадратная матрица порядка n	матрица, число строк которой равно числу ее столбцов и равно числу n
4	Главная диагональ квадратной матрицы А	образуется элементами с одинаковыми индексами а₁₁ , а₂₂ , …, а_mn
5	Транспонированная матрица	квадратная матрица, элементы которой симметричны относительно главной диагонали, равны а_ik = а_ki , i – 1,2,…,m; k= 1,2,…,n
6	Единичная матрица (Е)	квадратная матрица, на главной диагонали которой стоят единицы, а остальные элементы нулевые
7	Произведение матрицы А_mn (порядка mxn) на матрицу В_nk (порядка nxk)	матрица С_mk (порядка mxk), элементы которой вычисляются по формуле: С_ij = а_i1 b₁ _j + а_i2 b₂ _j +…+ а_in b_nj , i = 1,2,…,m; j = 1,2,…,k
8	Определитель квадратной матрицы А	число, которое ставится в соответствие матрице А и вычисляется по ее элементам
9	Алгебраическое дополнение А_ij элемента а_ij	величина А_ij = (-1)ⁱ⁺ ^j M_ij , где M_ij – определитель порядка (n-1), полученный вычеркиванием i-ой строки и j-го столбца, на пересечении которых стоит элемент а_ij
10	Вырожденная матрица	матрица, у которой определитель равен нулю
11	Обратная матрица для матрицы А	квадратная матрица А^-1 , которая удовлетворяет условию А^. А^-1 = А^-1. А = Е; обратная матрица А^-1 существует тогда и только тогда, когда исходная матрица невырожденная, detA¹ 0

К-во Просмотров: 516

Бесплатно скачать Реферат: Матрицы и определители 3

>>> Скачать <<<