Реферат: Оптимальные и адаптивные системы
![]() ,
,
т.к. начальные и конечные точки поменяли местами, то ![]() ,
, ![]() получим
получим
![]() , (*)
, (*)
аналогично
![]()
![]()
подставив (*), получим
 ,
,
отсюда
![]() .
.
Построим получившееся и по методу фазовой плоскости определим направление
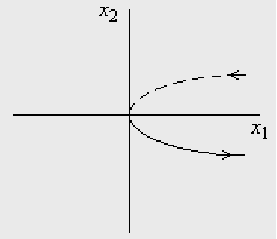
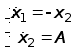
Применив метод непосредственного интегрирования, получим:
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() .
.
Функция будет иметь вид:
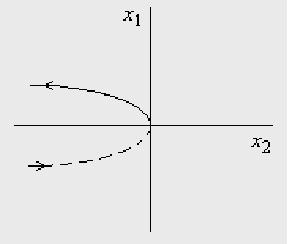
Изменив направление
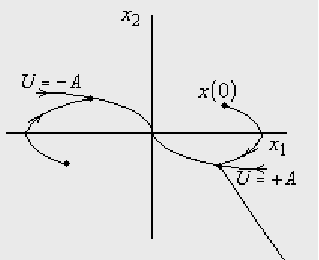
точка смены знака
(точка переключения)
Общее аналитическое выражение:
![]() .
.
Уравнение поверхности:
![]() .
.
Оптимальный закон управления: