Реферат: Основные понятия дифференциального исчисления и история их развития (Бакалавр)

х 3/2 3/2

х 3 3

х 4 4

= 2 + 9 ? 5 + 4 * 2 х + ? =

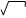
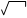= х ⁴ / 2 + 3х ³ – 10/3 х х + 8 х + С.

2.5. Метод замены переменной (способ подстановки).

ò

???????? ????? ??????? ?????????????? ??????? ???????? ?????? ???????????, ??????? ??????????? ?????, ????? ??????? ???????? f (х )dх ?? ???????? ?????????, ?? ????? ?? ????? ???? ???????????? ?????????????? ?? ????? ???? ?????? ? ??????????.

ò

ò

????? ??????????? ??????? ?? ?????????? ????????? ???????:

f (х )dх = f [j(t )]j’(t )dt, (1)

где х = j(t ) – дифференцируемая функция от t, производная которой j’(t ) сохраняет знак для рассматриваемых значений переменных.

ò

???????? ?????????? ???? ??????? ??????? ? ???, ??? ? ?????? ????????? f (х )dх ?????????? х ?????????? ?????????? t ?? ??????? х = j(t ) ?, ?????????????, dх ????????????? j?(t )dt.

ò

?????????????? ??????? (1) ????? ???????? ???? ????? ????????????????? ????? ?? ?????? ????????? ?????????? ?????????. ?????????????????? ????? ????? ???????, ?????

d [ f (х )dх ] = f(х)dх = f [j(t )] j’(t )dt

ò

?????????????????? ?????? ????? ???????, ?????

d f [j(t )] j’(t )dt = f [ j(t ) ] j’(t )dt

Таким образом, формула (1) справедлива. Часто употребляется обратная замена переменной, то есть, подстановка t = j(t ), dt = j’(t )dх.

ò

Примеры .

1) (2х + 3)⁴ dх.

Данный интеграл можно свести к табличному интегралу (V). Подстановка выбирается из простого соображения: в подынтегральном выражении табличного интеграла (V) в основании степени и под знаком дифференциала стоит одно и тоже выражение и .

ò

ò

ò

?????????????, ? ?????? ?????? ????? ????????? ??????????? и = 2х + 3, ?????? ????? dи = 2dх ? dх = dи /2, ? ??????

(2х + 3)5 10

(2х + 3)⁴ dх = и ⁴ (dи /2) = 1/2 и ⁴ dи =

= 1/2 * и ⁵ /5 + С = + С.