Реферат: Основные понятия дифференциального исчисления и история их развития (Бакалавр)
когда же зависимость переменной у от х даётся при помощи некоторой (промежуточной) функции и , то
у’х = f’(и)и’х .
При отыскании же дифференциалов получим в обоих случаях одинаковые формулы:
dх у = f’ (х ) dх х , dх у = f’ (и ) dх и
или
dу = f’ (х ) dх, dу = f’ (и ) dи.
1.4 Дифференциал суммы, произведения и частного.
Из теорем о производных суммы, произведения и частного можно получить аналогичные формулы для дифференциалов суммы, произведения и частного. Пусть и и J — функции от х:
и = f(х), J = j(х ),
имеющие непрерывные частные производные.
Если положить у = и + J,
то у’х = и’х + J’х ,
откуда у’х dх = и’х dх + J’х dх ,
следовательно dу = dи + d J,
то есть d (и + J) = dи + d J.
Аналогично dси = сdи,
где с – постоянное число;
|
|
d ( ) = .
Замечание. На практике часто бывает выгоднее оперировать дифференциалами, а потом делением на дифференциал независимой переменной переходить к производной.
1.5 Геометрическая интерпретация дифференциала.
 Дифференциал можно геометрически представить следующим образом:
Дифференциал можно геометрически представить следующим образом:
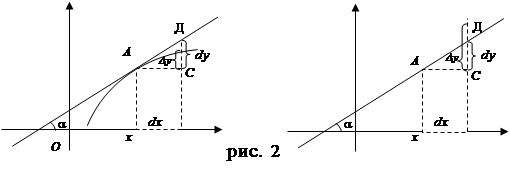
Из рис. 2 видно, что dу = f’ (х )dх = tg a . dх = СД.
Таким образом, если Dу – приращение ординаты кривой, то dу – приращение ординаты касательной.
|