Реферат: Основные понятия дифференциального исчисления и история их развития (Бакалавр)

Переходя к пределу получим: = 2х + = 2х .

Dу Dх

lim Dу = 0 Dх ®0

??? ????, ????? ????????? ????? ??????, ??????????, ????? , ?? ????, ????? ??????? ???.1

была непрерывной в точке х ⁰ .

Рассмотрим график функции у = f (х ) (рис.1)

Dу Dх

Легко заметить, что отношение равно тангенсу угла a, образованного положительным направлением секущей, проходящей через точки А и В (соответствующие точкам х и х +Dх ), с положительным направлением оси Ох, то есть, от А к В если теперь приращение Dх будет стремиться к нулю, точка В будет стремиться к А, то угол a будет стремиться к s, образованному положительным направлением касательной с положительным направлением оси Ох, а tg a будет стремиться к tg s.

lim Dу Dх ®0 Dх

??????? = tg s (????????????? ???????????? ??????????? ??????? ?? ???????????, ? ??????? ? ??????????).

Таким образом, можно утверждать следующее:

Производная в данной точке х равна тангенсу угла, образованного положительным направлением касательной в соответствующей точке (х ,f (х )) нашей кривой с положительным направлением оси Ох .

1.2 Дифференциальные функции. Определение дифференциала.

Определение. Функция у = f (х ) называется дифференцированной в точке х, если её приращение Dу в этой точке можно представить в виде

lim Dх ®0

Dу = f’ (х )Dх+ a(Dх )Dх,

где a (Dх ) = 0

Dу Dх

??? ????? ?? ?? ???????????, ??????????? ???????? ?????????????????? ???????? ????????????? ???????????. ??????????? ??? ??? ??????? ????? ? ??????????. ? ????? ???? ????? ?????????? у ? = f’ (х )

a(Dх)=

??????? ? f’ (х ), Dх ¹ 0

0 , Dх = 0

При таком определении a имеет для всех Dх

Dу = f’ (х )Dх +a(Dх )Dх .

lim Dх ®0

????????, ?????????????, ?????????? ????????????? a(Dх ) ??? Dх = 0, ?? ????, ????????? a (Dх ) = a(0) = 0, ??, ????????,

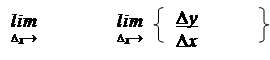a (Dх ) = – f’ (х ) = f’ (х ) – f’ (х ) = 0,

что и требовалось.