Реферат: Рациональные уравнения и неравенства

x ¹ 0

или

2x² + 11x + 2 = 0,

x ¹ 0;

X1 = 2; X2 = 1 / 2 или X3 = ( - 11 + Ö105) / 4; X4 = ( -11 - Ö105) / 4

(все найденные корни уравнения входят в область допустимых значений).

Ответ: 2; 0,5; ( - 11 + Ö105) / 4; (-11 - Ö105) / 4.

Пример 3.18. Решить уравнение x³ – x² – 9x – 6 = 0.

Решение. Угадаем хотя бы один корень данного уравнения. “Кандидатами” в целочисленные корни (а только их есть надежда отгадать) являются числа

±1, ±2, ±3, ±6.

Подстановкой в исходное уравнение убеждаемся, что X = -2 является его корнем.

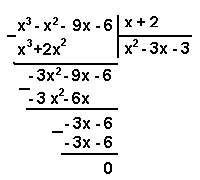???????? ????????? x³ ? x² ? 9x ? 6 ?? ??????? x + 2

x³ – x² – 9x – 6 = (x + 2)(x² – 3x – 3) = 0.

Решив теперь уравнение x² – 3x – 3 = 0,

получаем X₂ = (3 - Ö21) / 2, X₃ = (3 + Ö21) / 2.

Ответ: xÎ {-2; (3 - Ö21) / 2; (3 + Ö21) / 2}.

Пример 3.19.

x³ – x² – 8x + 6 = 0.

Решение. Здесь a_n = 1, a₀ = 6. Поэтому, если данное уравнение имеет рациональные корни, то их следует искать среди делителей числа 6: ±1, ±2, ±3, ±6. Проверкой убеждаемся, что x = 3, т.к. 27 – 9 – 24 + 6 = 0.

Делим (x³ – x² – 8x + 6) на (x – 3)

Получаем: x³ – x² – 8x + 6 = (x – 3)(x² + 2x – 2), т.е. данное уравнение можно представить в виде (x – 3)(x² + 2x – 2) = 0. Отсюда находим, что x₁ = 3 — решение, найденное подбором, x_2,3 = – 1 ±Ö3 — из уравнения x² + 2x – 2 = 0.

Ответ: x₁ = 3; x_2,3 = – 1 ±Ö3.

Пример 3.20.

4x⁴ + 8x³ + x² – 3x – 1 = 0.

Решение. Здесь a_n = 4, a₀ = –1. Поэтому рациональные корни уравнения следует искать среди чисел: ± 1; ± 0,5; ± 0,25 (делители 4 есть ±1; ±2; ±4, делители (– 1) есть ± 1). Если x = +1, то 4 + 8 + 1 – 3 – 1 ¹ 0; если x = – 0,5, то

4 / 16 – 8 / 8 + 1 / 4 + 3 / 2 – 1 = 0, т.е. x = – 0,5 корень уравнения. Делим

(4x⁴ + 8x³ + x² – 3x – 1) на (x + 0,5):

Данное уравнение можно представить в виде:(x + 0,5)(4x³ + 6x² – 2x – 2) = 0.

Отсюда x₁ = – 0,5 (решение, найденное подбором) и 4x³ + 6x² – 2x – 2 = 0, т.е. 2x³ + 3x² – x – 1 = 0. Аналогично находим корень этого уравнения:x = – 0,5. Снова делим.

Имеем: (x + 0,5)(2x² + 2x – 2) = 0. Отсюда x₂ = – 0,5 и x_3,4 = (– 1 ±Ö5) / 2.