Реферат: Уравнения математической физики

§ 1.Тема. Некоторые определения и обозначения.

Определение.

Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции. Если неизвестная функция зависит от одной переменной, то это обыкновенное дифференциальное уравнение, иначе - уравнение в частных производных.

Определение.

Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения.

Определение.

Дифференциальное уравнение называется линейным, если производные и сама неизвестная функция входят в уравнение линейным образом.

(1)

Пусть выбран любой, где , и его норма:

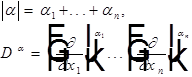- дифференциальный оператор.

- запись линейного диф. уравнения с помощью диф. оператора. (2)

Определение.

Открытое, связное множество называется областью.

По умолчанию будем считать область ограниченной.

Через или будем обозначать границу области.

Определение.

- (n-1)-мерное многообразие S в принадлежит классу (), если

для и такие, что:

, где

однозначно проектируется на плоскость , при этом:

D - проекция данного множества на плоскость , - k раз непрерывно дифференцируема в D по всем переменным.

Можно разбить поверхность на части, в каждой части можно одну координату выразить через другие непрерывно дифференцируемой функцией.

- множество k раз непрерывно дифференцируемых функций в Q.

- множество k раз непрерывно дифференцируемых функций в .

, аналогично .

- множество финитных k раз непрерывно дифференцируемых функций.

Аналогично: .

§ 2. Классификация линейных уравнений в частных производных второго порядка.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--