Реферат: Уравнения математической физики

Любая функция из сколь угодно точно аппроксимируема своими осреднениями - бесконечно дифференцируемыми, финитными в .

Доказательство.

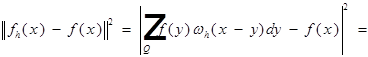
От Q к , от к

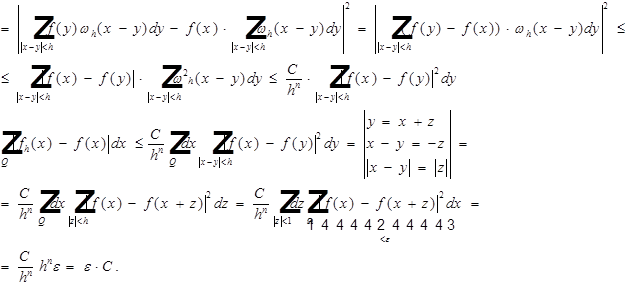
При .

Возьмем любые две функции:

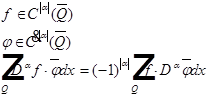
Определение.

- множество функций, принадлежащих на любом компакте внутри области.

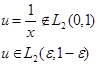
Определение 1.

Пусть

- обобщённая производная функции f , если выполняется:

(1)

Теорема 1.

Обобщённая производная определяется единственным образом.

Доказательство.

Предположим противное: - обобщённые производные функции f .

(2)

(3)

(2),(3) - тождество для

- что и требовалось доказать.

Теорема 2.

Обобщённые производные не зависят от порядка дифференцирования.

Доказательство - из интегрального тождества (1).

Примеры обобщённых производных.

Ex 1.