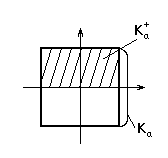
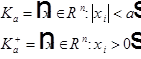Реферат: Уравнения математической физики

Выберем и рассмотрим

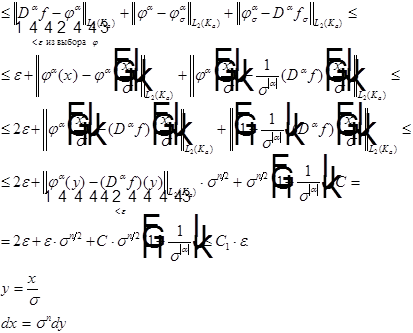
Разбиение единицы.

Теорема.

Пусть - ограниченная область, пусть - покрытие замыкания Q , - может равняться бесконечности.

- открытые, тогда: существует конечный набор - финитные, бесконечно дифференцируемые в , неотрицательные функции, такие, что:

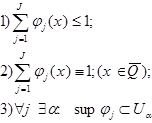
Используется для локализации свойства: U имеет свойство на , расширяем D на путём домножения на .

Доказательство.

Возьмём . Для - y покрывается множеством .

Для каждой выбранной y построим:

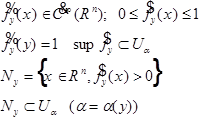
покрывается . Из бесконечного покрытия выберем конечное подпокрытие:

.

Обозначим: . Обозначим: .

Определим: :

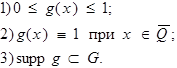
Получили: .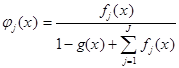

Если , то , , и .

Знаменатель в 0 не обращается.

Построена

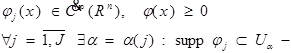выполняется свойство 3.

- выполняются свойства 1 и 2.

Теорема о разбиении единицы доказана.

Теорема о продолжении функции.

Частный случай - продолжение из прямоугольников.