Реферат: Уравнения математической физики

По определению:

Пусть и

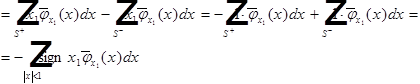
Ex 2.

Покажем, что обобщённой производной не существует.

Пусть , то:

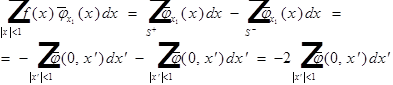
где

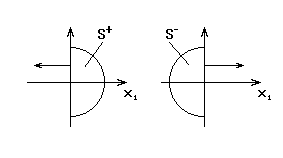
1) пусть носитель в , то :

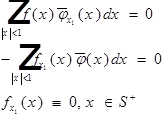
2) пусть : , значит:

Вывод: .

Вывод: , не имеет обобщённой производной.

Теорема 3.

Пусть имеет обобщённую производную , то:

1. (4)

если .

2. Если к тому же

(6)

(7)

Доказательство.

Выберем h так, чтобы