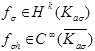Реферат: Уравнения математической физики

в .

в .

Интегральное тождество для :

Из сильной сходимости следует слабая:

Вывод: пространство полное.

Свойства пространств Соболева.

1. для .

2.Если , то .

3.Если , то .

4.Если , то

если , то .

5. - невырожденное, k раз непрерывно дифференцируемое преобразование, отображающее в .

и пусть .

Пусть .

Пусть , то .

Утверждение.

Невырожденная, гладкая замена переменных сохраняет принадлежность функции пространству Соболева.

6.Обозначим - куб со стороной 2a с центром в начале координат.

Множество бесконечно дифференцируемых функций замыкания куба является всюду плотным в .

.

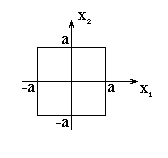
Доказательство.

Раздвинем область, возьмём и будем её аппроксимировать последовательностью бесконечно гладких функций.

(определена в растянутом кубе)