Реферат: Уравнения математической физики

Рассмотрим - финитная, бесконечно дифференцируема в .

Значит, .

Аппроксимация получена.

Теорема 2.

Множество непрерывных функций всюду плотно в пространстве .

Определение 2.

Пусть и считается продолженной нулем вне Q . Скажем:

f - непрерывна в среднеквадратичном, если :

.

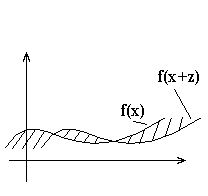
Теорема 3.

Любая функция из непрерывна в среднеквадратичном.

Доказательство.

Пусть . Пусть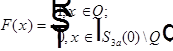

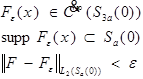
Оценим:

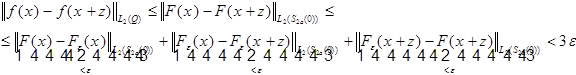
При сдвиге supp сдвигается в пределах шара радиуса 2a.

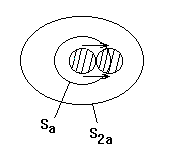
Теорема доказана.

Определение 3.

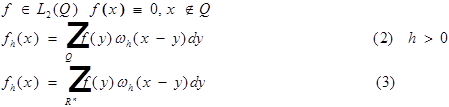
- бесконечно дифференцируема, финитна.

Свойства:

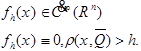
- осреднение функции f .