Реферат: Уравнения математической физики
Пусть 
- ограниченная область
, 
- всюду плотно в 
.
Доказательство.
Рассмотрим произвольную функцию 
.
- ограниченная.
F -продолжение f. Так как F - финитная в , то 
Сепарабельность пространств Соболева.
Теорема.
Пусть - ограниченная область, 
, тогда :
- сепарабельное.
Построениe счётного всюду плотного множества.
Доказательство.
Рассмотрим 
; продолжение функции f : 
.
Аппроксимируем функцию F . Множество финитных, бесконечно дифференцируемых функций (в силу свойств осреднений) всюду плотно в пространстве финитных функций 
.
Очевидно : 
.
Где коэффициенты : 
.
Пусть H - сепарабельное гильбертово пространство.
Определение.
Функции 
образуют ортонормированную систему, если 
, и 
.
Утверждение.
В каждом сепарабельном гильбертовом пространстве существует ортонормированный базис, т.е. такая система ,что 
.
Разложение по этому базису единственно, и : 
.
Равенство Парсеваля.
.
Пространство 
- сепарабельное гильбертово пространство с ортонормированным базисом : можно взять систему экспонент (нормированную).
Разложение в сходящийся ряд :
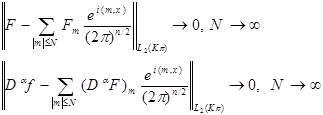
Определим вид коэффициентов Фурье:
проинтегрируем по частям и получим :
, где 
Получаем :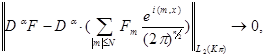 
и следовательно :
F можно точно аппроксимировать линейными комбинациями экспонент.
Искомое множество - линейное пространство экспонент с рациональными коэффициентами.
След функции из H k(Q).
Для функции из
понятие значения на (n-1)- мерной поверхности не определено.
Если 
удовлетворяет условиям дифференцируемости, то :
определение следа функции на (n-1)- мерной поверхности.
Рассмотрим 
-ограниченную область, 
.
- (n-1) - мерная поверхность, 
.
Пусть 
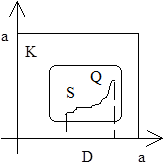
Можно разбить на конечное число простых кусков, однозначно проецирующихся на координа тные плоскости и описывающиеся уравнением : 
Для любой непрерывной функции след - её значение на поверхности, однозначно продолженое по непрерывности.
Так как f=0 вне области Q , то по формуле Ньютона-Лейбница :
Оценим :
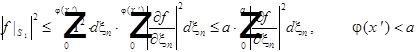
Обе части умножим на 
и проинтегрируем по D :
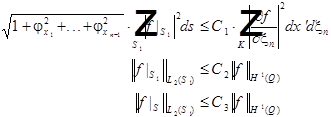
f - финитная.
Так как 
может быть продолжена в 
финитным образом,
, причём 
Существует последовательность 
Отсюда следует фундаментальность последовательности следов в 
- полное, следовательно
- сходится,