Сочинение: Доказательство утверждения, частным случаем которого является великая теорема Ферма

, ,

где - взаимно простые нечетные целые числа.

*******

Случай 2

Нетрудно догадаться, что если бы у уравнения (15) были бы решения, противоположные по знаку с решениями (16), (17′), (18) и (19), мы бы получили, в конечном итоге, решения, противоположные по знаку решениям (39), (37), (38) и (33), т.е.

, ,

, ,

где - взаимно простые нечетные целые числа .

*******

Случай 3

(16)

(17′)

(18)

(19′).

Тогда сумма имеет вид:

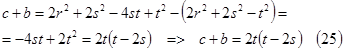
Учитывая (14) и (19′), можно получить разность :

- => (26′).

Выразим из (25) и (26′) :

=>

=> .

По условию должны быть взаимно простыми целыми нечетными числами , поэтому их общий множитель .

Т.о., имеют вид :

(30′), (31′), а их сумма .

Т.к. из (8) , то => .

Из (19´) с учетом (29) выразим :

, т.е. (33´).

Т.о., , ,

где ,