Сочинение: Доказательство утверждения, частным случаем которого является великая теорема Ферма

(19)

Тогда сумма имеет вид:

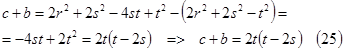
Учитывая (14) и (19), можно получить разность :

=> .

Выразим из (25) и (26) :

=>

=> .

По условию должны быть взаимно простыми целыми числами , поэтому их общий множитель .

Т.о., имеют вид:

, , а их сумма .

Т.к. из (8) , то => .

Из (19) с учетом (29) выразим :

, т.е. .

Т.о., , , т.е.

,

выражения которых, с учетом (33), полностью совпадают с (9) и (10).

Теперь, с учетом (17′) и (18), найдем сумму :

т.к. , т.е. .

(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (29 ). В последующих действиях мы это учтем).

Теперь, учитывая (32), получим значение для b :

, т.к. из (29) вытекает .

Итак, .

Учитывая (35), получим => .

Теперь, с учетом (38),можно получить окончательное выражение для с (из (34)):

, т.е. .

Таким образом, уравнение (15) , решениями которого являются (16), (17′), (18) и (19), в конечном счете имеет следующие решения: