Сочинение: Три задачи по теории чисел
Три задачи по теории чисел
Задача 1
Утверждение 1
Пусть р1 , р2 и р3 являются ненулевыми рациональными числами, причем р1 + р2 = р3. Тогда произведение р1 * р2 * р3 не является точным кубом никакого (отличного от нуля) рационального числа, то есть р1 * р2 * р3 ≠ R3 , где R – некоторое рациональное число (R ≠ 0).
Доказательство
Положим
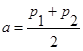и 
Очевидно, что а (а≠0) и b - рациональные числа, так как рациональными являются числа р1 и р2 .
(Если а=0, т.е. р1 = - р2 , то р1 + р2 = р3 = 0, что противоречит нашему утверждению (р3 
0).
Если b=0, т.е. р1 = р2 , то р3 = 2 р1 
р1 * р2 * р3 = р1 * р1 * 2р1 =2р
, т.е. 
р1 * р2 * р3 = 2р≠ R3 и противоречие с нашим утверждением отсутствует.)
Тогда имеем:
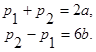
Теперь нетрудно выразить старые переменные через новые:
(1) 
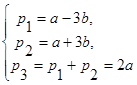
Таким образом, замена р1 и р2 на a и b является обратимой (число Р3 в обоих случаях является зависимой переменной).
Предположим теперь, что Утверждение 1 неверно, и число 
является точным кубом (R3 ) некоторого рационального числа R (R ≠ 0) .
Обозначим 
(2), где r0, т.к. при r = 0 либо р1 =0, либо р2 =0, либо р3 =0.
где q0 (пояснение ниже).
Числа r и q являются рациональными числами, если рациональны числа a и b. Далее имеем:
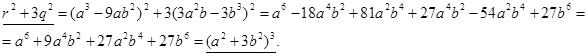
Пояснение
При q=0 
, где r0 0 - рациональное число (т.к. r0).
Из (2) следует 
, откуда R не является рациональным числом, что противоречит условию. Следовательно, q0.
Отсюда число 
является кубом некоторого ненулевого рационального числа , обозначим это число через 
(3), где С0 (С > 0).
Обозначим: 
, тогда:
(с учетом (2) и (3))
(4)
Так как r, q – рациональные числа, то и числа A, B, (CR) -также рациональны числа.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--