Учебное пособие: Комплексные числа
![]() ;
;
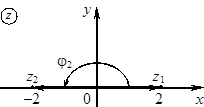
5)![]() ,
,
![]() ;
;
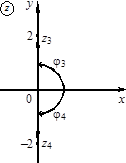
6)![]() ,
,
то есть для z = 0 будет
![]() , j не определен.
, j не определен.
Арифметические действия над комплексными числами (Дайте определения и перечислите основные свойства арифметических действий над комплексными числами. )
Сложение (вычитание) комплексных чисел
z 1 ±z 2 = (x 1 + iy 1) ± (x 2 + iy 2) = (x 1 ±x 2) + i (y 1 ±y 2),(5)
то есть при сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и мнимые части.
Примеры
1)(1 + i ) + (2 – 3i ) = 1 + i + 2 –3i = 3 – 2i ;
2)(1 + 2i ) – (2 – 5i ) = 1 + 2i – 2 + 5i = –1 + 7i .
Основные свойства сложения
1)z 1 + z 2 = z 2 + z 1;
2)z 1 + z 2 + z 3 = (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3);
3)z 1 – z 2 = z 1 + (– z 2);
4)z + (–z ) = 0;
5)![]() .
.
Умножение комплексных чисел в алгебраической форме
z 1∙z 2 = (x 1 + iy 1)∙(x 2 + iy 2) = x 1x 2 + x 1iy 2 + iy 1x 2 + i 2y 1y 2 = (6)
= (x 1x 2 – y 1y 2) + i (x 1y 2 + y 1x 2),
то есть умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой ![]() и приведением подобных по действительным и мнимым слагаемым.
и приведением подобных по действительным и мнимым слагаемым.
Примеры
1)(1 + i )∙(2 – 3i ) = 2 – 3i + 2i – 3i 2 = 2 – 3i + 2i + 3 = 5 – i ;
2)(1 + 4i )∙(1 – 4i ) = 1 – 42 i 2 = 1 + 16 = 17;
3)(2 + i )2 = 22 + 4i + i 2 = 3 + 4i .
Умножение комплексных чисел тригонометрической форме
z 1∙z 2 = r 1(cosj 1 + i sinj 1)×r 2(cosj 2 + i sinj 2) =
= r 1r 2(cosj 1cosj 2 + i cosj 1sinj 2 + i sinj 1cosj 2 + i 2 sinj 1sinj 2) =
= r 1r 2((cosj 1cosj 2 – sinj 1sinj 2) + i (cosj 1sinj 2 + sinj 1cosj 2))