Учебное пособие: Комплексные числа

Произведение комплексных чисел в тригонометрической форме , то есть при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.

Пример

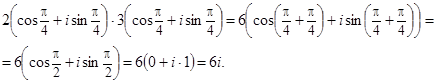
Основные свойства умножения

1)z 1×z 2 = z 2×z 1 — коммутативность;

2)z 1×z 2×z 3 = (z 1×z 2)×z 3 = z 1×(z 2×z 3) — ассоциативность;

3)z 1×(z 2 + z 3) = z 1×z 2 + z 1×z 3 — дистрибутивность относительно сложения;

4)z ×0 = 0; z ×1 = z ;

5).

Деление комплексных чисел

Деление — это обратная умножению операция, поэтому

если z ×z 2 = z 1 и z 2 ¹ 0, то .

При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю:

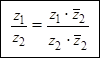Деление комплексных чисел в алгебраической форме .(7)

При выполнении деления в тригонометрической форме модули делятся, а аргументы вычитаются:

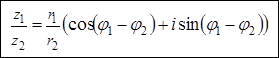Деление комплексных чисел в тригонометрической форме .(8)

Примеры

1);

2).

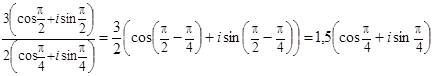Возведение комплексного числа в натуральную степень

Возведение в натуральную степень удобнее выполнять в тригонометрической форме:

В результате получается формула Муавра :

Формула Муавра,(9)

то есть при возведении комплексного числа в натуральную степень его модуль возводится в эту степень, а аргумент умножается на показатель степени.

Пример

Вычислить (1 + i )10.

Решение:

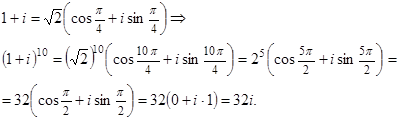
Замечания