Учебное пособие: Комплексные числа
1)
;
2)
;
3) 
.
Действия над комплексными числами в показательной форме выполняются по правилам действий со степенями:
,(12)
,(13)
,(14)
, 
.(15)
Примеры
Пусть 
,
.
Тогда 
;
;
;
, 
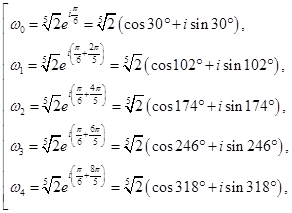
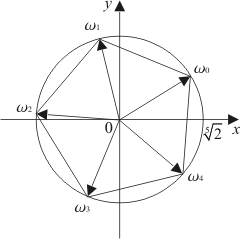
Числа 
являются вершинами правильного пятиугольника, вписанного в окружность радиуса 
.
Формулы Эйлера
Используем определение 
Þ
,
так как 
, 
.
Из этих равенств следуют формулы Эйлера
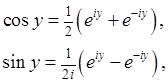Формулы Эйлера(16)
по которым тригонометрические функции 
и 
действительной переменной 
выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.
§ 2. Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел
Целой функциейили алгебраическим многочленом (полиномом ) аргумента x называется функция вида
.(1)
Здесь n – степень многочлена ( натуральное число или 0),
x – переменная (действительная или комплексная),
a 0, a 1, …, an –коэффициенты многочлена (действительные или комплексные числа),причем, a 0¹ 0