Учебное пособие: Комплексные числа

Это тождество тоже верно при "x , в том числе при x = 0

Þ полагая x = 0, получим аn – 1 = bn – 1.

Взаимно уничтожим в (3') слагаемые аn – 1 и a n – 1 и поделим обе части на x , в результате получим

.

Аналогично продолжая рассуждение, получим, что аn – 2 = bn –2, …, а 0 = b 0.

Таким образом, доказано, что из тождественного равенства 2-x многочленов следует совпадение их коэффициентов при одинаковых степенях x .

Обратное утверждение справедливо очевидно, т.е. если два многочлена имеют одинаковыми все коэффициенты, то они есть одинаковые функции, следовательно, их значения совпадают при всех значениях аргумента, что и означает их тождественное равенство. Свойство 1 доказано полностью. v

Пример

при .

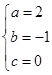Свойство 2 ( о делении многочлена на разность (x – х0) )

Теорема Безу

При делении многочлена Pn (x ) на разность (x – х 0) получается остаток, равный Pn (x 0), то есть

Теорема Безу,(4)

гдеQn – 1(x ) — целая часть от деления, является многочленом степени (n – 1).

Доказательство

w Запишем формулу деления с остатком:

Pn (x ) = (x – х 0)∙Qn – 1(x ) + A ,

гдеQn – 1(x ) — многочлен степени (n – 1),

A — остаток, который является числом вследствие известного алгоритма деления многочлена на двучлен «в столбик».

Это равенство верно при "x , в том числе при x = х 0 Þ

Pn (x 0) = (x 0 – x 0)×Qn – 1(x 0) + A Þ

A = Pn (х 0), ч.т.д. v

Следствие из теоремы Безу. О делении многочлена на двучлен без остатка

Если число х 0 является нулем многочлена, то этот многочлен делится на разность (x – х 0) без остатка, то есть

Þ .(5)

Примеры

1) , так какP 3(1) º 0

Þ.

2) , так какP 4(–2) º 0