Учебное пособие: Основы теории вероятности
Решение. В качестве гипотезы примем:
Н1 = {выбранный наугад человек со средним образованием};
Н2 = { выбранный наугад человек со высшим образованием }.
Р(Н1 ) = 0,7; Р(Н2 ) = 0,3.
Пусть соб. А = {выбранный наудачу человек безработный}, тогда
P(A/H1 ) = 0,1, P(A/H2 ) = 0,02.
Нужно определить P(![]() ) по формуле (4.2).
) по формуле (4.2).
Имеем:

Задача №54. На сборочный конвейер поступили детали с 3-х станков, производительность которых неодинакова: I-го – 50% плана, II-го – 30% плана, III-го – 20% плана. Вероятность получения годного узла равна 0,92, если деталь I-го станка, 0,95,если деталь со II-го станка, 0,82, если деталь с III-го станка. Определить вероятность того, что в сборку попали детали, изготовленные на первом станке, если узел годный.
Решение. А = { узел годный};
Н1 = {деталь с I-го станка};
Н2 = {деталь со II-го станка};
Н3 = {деталь с III-го станка};
Р(Н1 )=0,5; Р(Н2 )=0,3; Р(Н3 )=0,2.
Р(А/Н1 )=0,92; Р(А/Н2 )=0,95; Р(А/Н3 )=0,82.

Задача №55. 30% приборов собирают специалисты высокой квалификации, 70% - средней квалификации. Надёжность работы прибора, собранного специалистом высокой квалификации – 0,9, а специалистом средней квалификации – 0,8. Взятый наугад прибор оказался надёжным. Определить вероятность того, что прибор собран специалистом высокой квалификации.
Решение.
Пусть событие А = {прибор работает безотказно}.
До проверки прибора возможны 2 гипотезы:
Н1 = {прибор собран специалистом высокой квалификации};
Н2 = { прибор собран специалистом средней квалификации }.
Р(Н1 ) = 0,3, Р(Н2 ) = 0,7.
Условные вероятности события А равны:
P(A/H1 ) = 0,9, P(A/H2 ) = 0,8.
Пусть событие А произошло, тогда
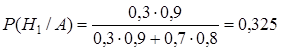 .
.
Задача №56. Из 10 учащихся, которые пришли на экзамен по математике (нужно было подготовить 20 вопросов), трое подготовились на отлично (выучив по 20 вопросов), четверо – на хорошо, выучив по 16 вопросов, двое – на удовлетворительно, выучив по 10 вопросов, один не готовился и может ответить на 5 вопросов из 20. В билете 3 вопроса. Первый ученик ответил на все 3 вопроса своего билета. Какова вероятность того, что этот ученик подготовился на отлично?