Учебное пособие: Разложение функций. Теория вероятностей

Функциональные ряды (ФР). Степенные ряды (СтР)

Функциональный ряд – ряд вида

,

члены которого являются функциями от х.

Придавая х различные числовые значения, получаем различные числовые ряды, которые могут сходиться или расходиться.

Совокупность тех значений х, при которых ФР сходится, называется областью сходимост и этого ряда. Область сходимости ФР чаще всего служит какой-нибудь промежуток оси ОХ.

Частным случаем ФР является степенной ряд.

СтР – ФР вида

,

где а,С0,С1,…,Сn – постоянные числа, называемые коэффициентами ряда. При а=0 СтР принимает вид:

Для всякого СтР существует такой интервал, который называется интервалом сходимости, внутри которого ряд сходится абсолютно; вне этого интервала ряд расходится.

Задан СтР, надо найти интервал сходимости для этого ряда. Находим так:

- радиус сходимости ряда СтР.

-R<x-a<R

a-R<x<a+R

Если взять любое значение х из интервала сходимости (расходимости) и подставить его в СтР вместо х, то получим сходящийся (расходящийся) числовой ряд.

В частном случае R может быть равен 0 (R=0) или (R=).

Если R= то интервал сходимости будет от - до + (-;+), т.е. ряд сходится на всей числовой оси.

Если R=0 то ряд расходится на всей числовой оси, кроме точки х=а (в этой точке ряд сходится).

Для нахождения R СтР применяем формулы Да Ламбера или Коши:

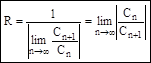- формула ДаЛамбера

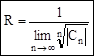- формула Коши

На концах интервала сходимости, т.е. в точках х=а-R и х=а+R вопрос о сходимости/расходимости данного ряда решается индивидуально для каждого конкретного ряда. Для этого необходимо подставить с СтР вместо х числа х=а-R и х=а+R и исследовать полученные числовые ряды на сходимость или расходимость. Если ряд сходится (расходится), то интервал сходимости будет закрытым (открытым).

ИТОГ . Задан СтР. Найти интервал сходимости СтР.

1. Найти R. 2. определить интервал сходимости. 3. исследовать на сходимость концы интервалов.

Ряды Тейлора и Макларена

Всякая функция, бесконечно дифференцируемая в интервале (т.е. a-R<x<a+R), может быть разложена в этом интервале в сходящийся к ней степенной ряд по степеням х-а , который называется рядом Тейлора и имеет вид:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--