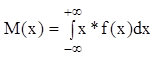Учебное пособие: Разложение функций. Теория вероятностей
Геометрически, равенство F(x)=Р(X<x) можно растолковать: F(x) есть вероятность того, что НСВ Х примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Свойства ИФ.
1. Значение ИФ принадлежит промежутку [0;1], т.е. F(x)![]() .
.
2. ИФ есть неубывающая функция, т.е. х2>х1,![]() .
.
Следствие 1. Вероятность того, что НСВ Х примет значение, заключенное в интервале (а;в), равна приращению интегральной функции на этом интервале, т.е.
P(a<x<b)=F(b)-F(a)
Следствие 2. Вероятность того, что НСВ Х примет одно определенное значение, например, х1=0, равна 0, т.е. Р(х=х1)=0.
3. Если все возможные значения НСВ Х принадлежат (а;в), то F(x)=0 при x<а, и F(x)=1 при х>в.
Следствие 3. Справедливы следующие предельные отношения.
Дифференциальная функция распределения (ДФР) вероятностей непрерывной случайной величины (НСВ) (плотность вероятности).
ДФ f(x) распределения вероятностей НСВ называют первую производную от ИФР :
f(x)=F’(x)
Часто вместо ФДР говорят плотность вероятности (ПВ).
Из определения следует, что, зная ИФ F(x) можно найти ДФ f(x). Но выполняется и обратное преобразование: зная ДФ f(x), можно найти ИФ F(x).
 ;
;
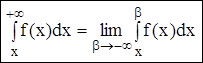 ;
;
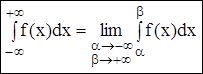
Вероятность того, НСВ Х примет значение, принадлежащее (а;в), находится:
А). Если задана ИФ – следствие 1.
Б). Если задана ДФ
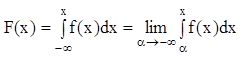
Свойства ДФ.
1. ДФ – не отрицательная, т.е. ![]() .
.
2. несобственный интеграл от ДФ в пределах (![]() ), равен 1, т.е.
), равен 1, т.е. ![]() .
.
Следствие 1. Если все возможные значения НСВ Х принадлежат (а;в), то ![]() .
.
Примеры. №263, 265, 266, 268, 1111, 272, д/з.
Числовые характеристики НСВ.
1. Математическое ожидание (МО) НСВ Х, возможные значения которой принадлежат всей оси ОХ, определяется по формуле: