Учебное пособие: Разложение функций. Теория вероятностей

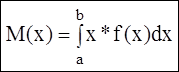
Все свойства МО, указанные для дискретных величин, сохраняются и для непрерывных величин.

2. Дисперсия НСВ Х, возможные значения которой принадлежат всей оси ОХ, определяется по формуле:

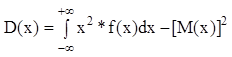
Если все возможные значения НСВ Х принадлежат (а;в), то дисперсия определяется по формуле:

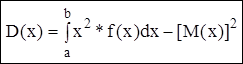
Все свойства дисперсии, указанные для дискретных величин, сохраняются и для непрерывных величин.

3. Среднее квадратичное отклонение НСВ Х определяется также, как и для дискретных величин:

Примеры. №276, 279, Х, д/з.

Операционные исчисления (ОИ).

ОИ представляет собой метод, позволяющий свести операции дифференцирования и интегрирования функций к более простым действиям: умножение и деление на аргумент так называемых изображений этих функций.

Использование ОИ облегчает решение многих задач. В частности, задач интегрирования ЛДУ с постоянными коэффициентами и систем таких уравнений, сводя их к линейным алгебраическим.

Оригиналы и изображения. Преобразования Лапласа.

f(t)-оригинал; F(p)-изображение.

Переход f(t)F(p) называется преобразование Лапласа .

Преобразование по Лапласу функции f(t) называется F(p), зависящая от комплексной переменной и определяемая формулой:

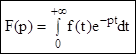
Этот интеграл называется интеграл Лапласа. Для сходимости этого несобственного интеграла достаточно предположить, что в промежутке f(t) кусочно непрерывна и при некоторых постоянных М>0 и удовлетворяет неравенству

Функция f(t), обладающая такими свойствами, называется оригиналом , а переход от оригинала к его изображению, называется преобразованием Лапласа .

Свойства преобразования Лапласа.

Непосредственное определение изображений по формуле (2) обычно затруднено и может быть существенно облегчено использованием свойств преобразования Лапласа.

Пусть F(p) и G(p) являются изображениями оригиналов f(t) и g(t) соответственно. Тогда имеют место следующие свойства-соотношения:

1. С*f(t)С*F(p), С=const -свойство однородности.

2. f(t)+g(t)F(p)+G(p) –свойство аддитивности.

3. f(t)F(p-) -теорема смещения.

4.

переход n–ой производной оригинала в изображение (теорема дифференцирования оригинала).