Учебное пособие: Разложение функций. Теория вероятностей
![]()
![]()
5. y”+py’+qy=0; f(x)=eax Pn ’(x)
![]()
Теорема дифференцирования изображения
Таблица изображений основных элементарных функций. Нахождение изображений по оригиналу (переход от оригинала к изображению).
| 1 | 1 | 5 | tn | 9 | |
| 2 | C | 6 | |||
| 3 | 7 | 10 | |||
| 4 | t | 8 |
Нахождение оригинала по изображению (обращение изображения - ОИ).
Отыскание оригинала по известным изображениям называется обращением изображения.
В простейших случаях эта операция выполняется с помощью таблицы и свойств преобразования Лапласа. При интегрировании дифференциальных уравнений возникает необходимость обращать правильные рациональные дроби. Всякую рациональную дробь можно разложить на сумму простейших дробей вида:
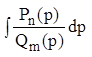
А).A/(p-a); Б).A/(p-a)n ; В).(Ap+B)/(p2 +pa+b); Г). (Ap+B)/(p2 +pa+b)2